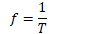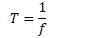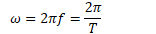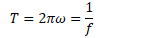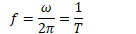Simple Harmonic Motion
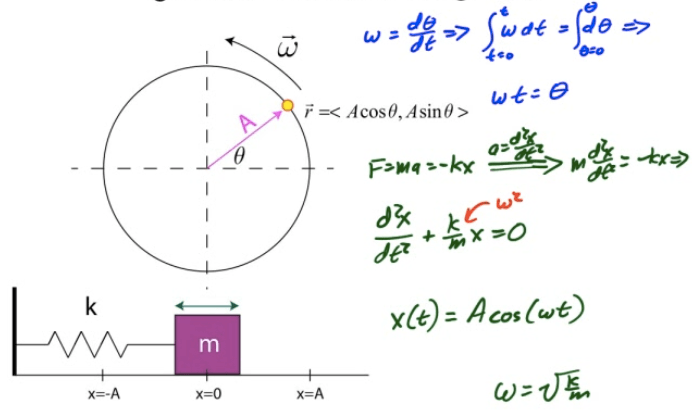
Simple harmonic motion (SHM) is motion in which a restoring force is directly proportional to the displacement of an object
Nature's response to a perturbation or disturbance is often SHM
Circular Motion vs. SHM
Position, Velocity, Acceleration
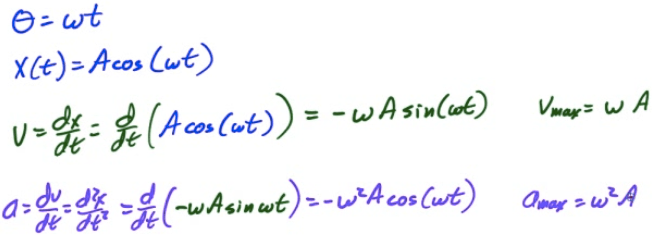
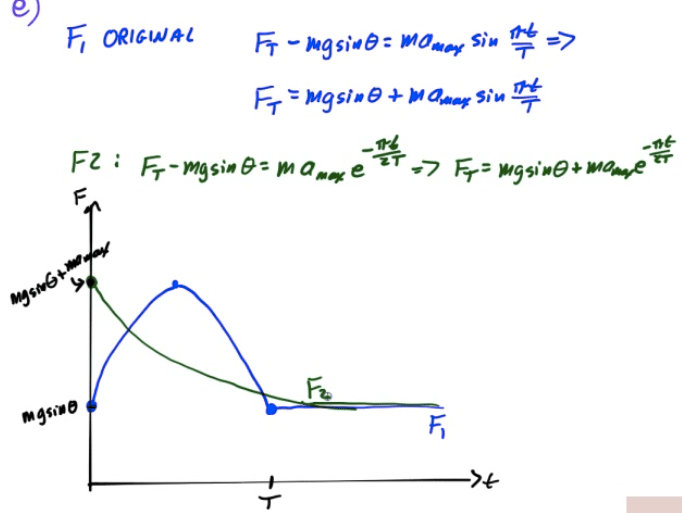
Frequency and Period
Frequency
Frequency is the number of revolutions or cycles which occur each second
Symbol is f
Units are 1/s, or Hertz (Hz)
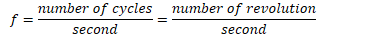
Period
Period is the time it takes for one complete revolution, or cycle.
Symbol is T
Unites are seconds (s)
T = time for 1 cycle = time for 1 revolution
Relationship
Angular Frequency
Angular frequency is the number of radians per second, and it corresponds to the angular velocity for an object traveling in uniform circular motion
Relationship
Example 1: Oscillating System
An oscillating system is created by a releasing an object from a maximum displacement of 0.2 meters. The object makes 60 complete oscillations in one minute
Determine the object's angular frequency
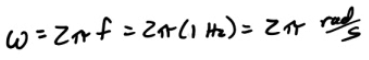
What is the object's position at time t=10s?

At what time is the object at x=0.1m?
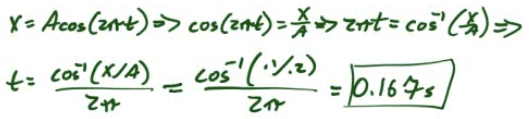
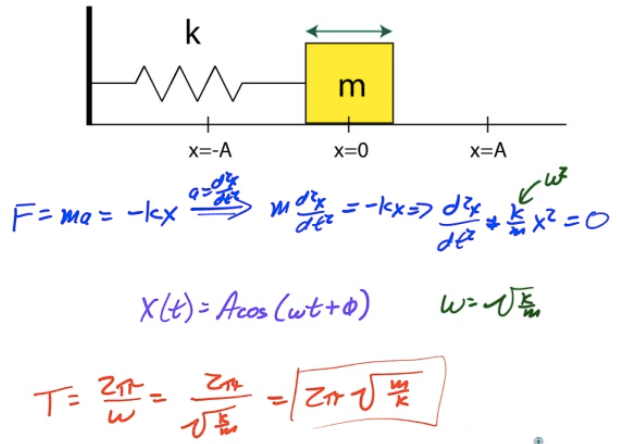
Mass on a Spring
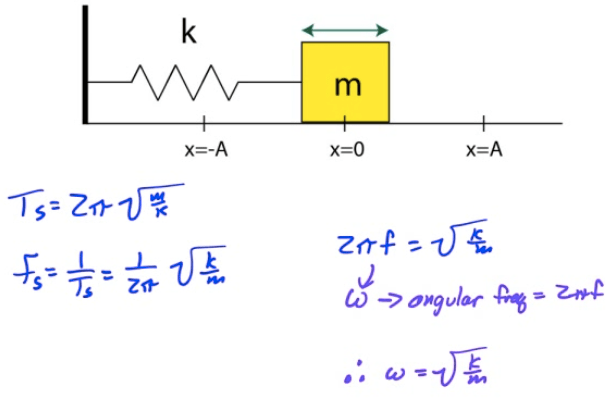
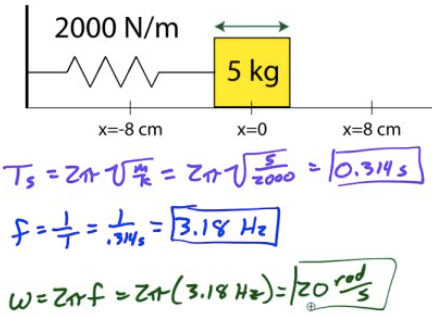
Example 2: Analysis of Spring-Block System
A 5-kg block is attached to a 2000 N/m spring as shown and displaced a distance of 8 cm from its equilibrium position before being released.
Determine the period of oscillation, the frequency, and the angular frequency for the block
General Form of SHM
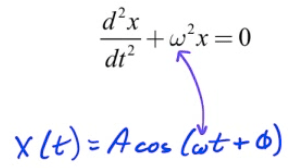
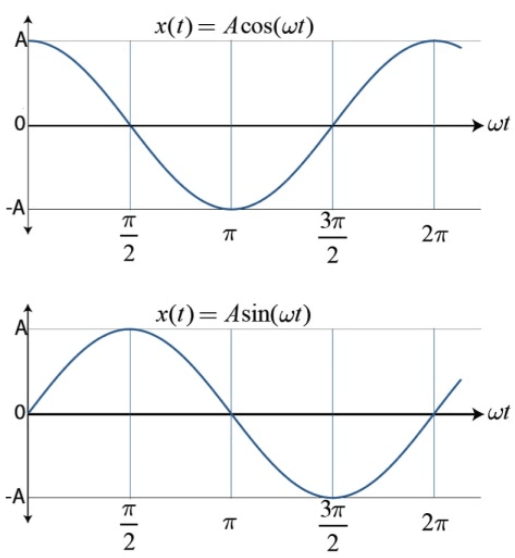
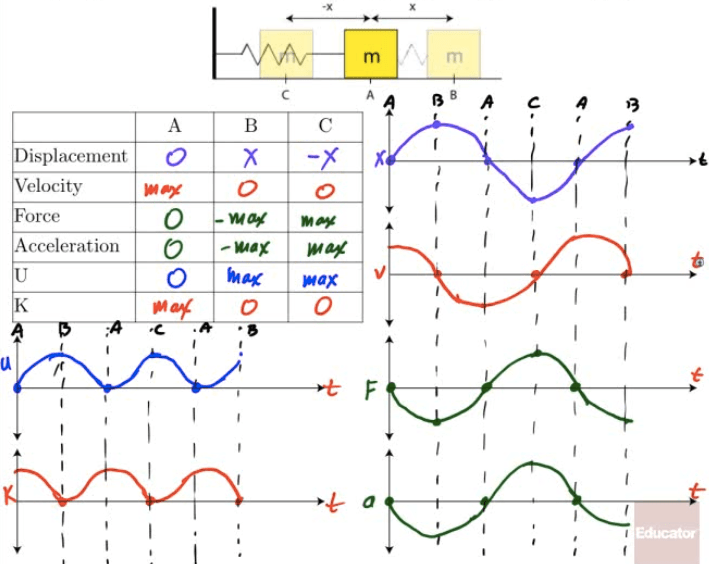
Graphing SHM
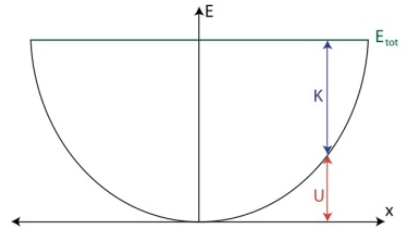
Energy of SHM
When an object undergoes SHM, kinetic and potential energy both vary with time, although total energy (E=K+U) remains constant
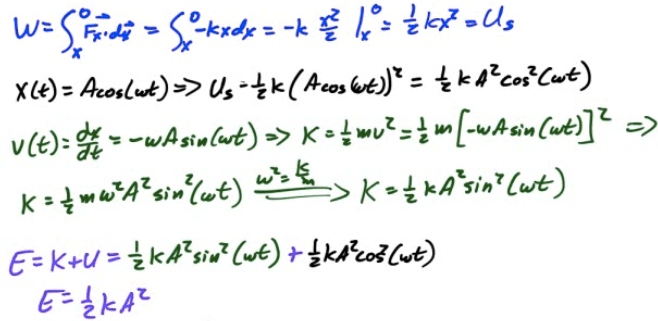
Horizontal Spring Oscillator
Vertical Spring Oscillator
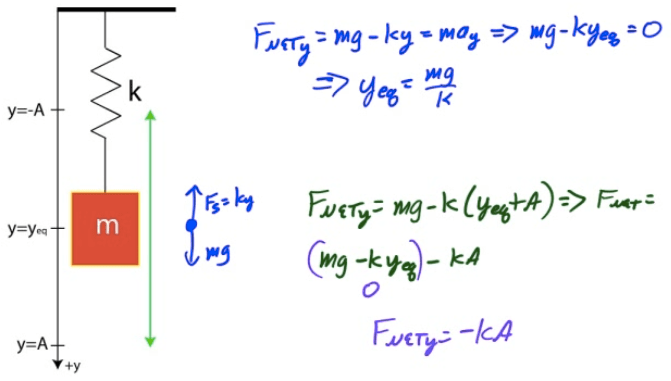
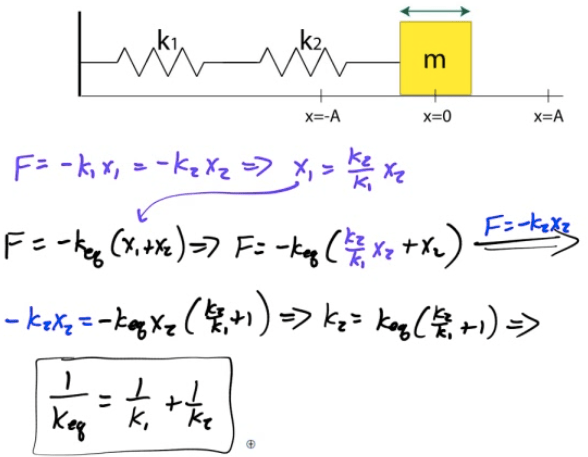
Springs in Series
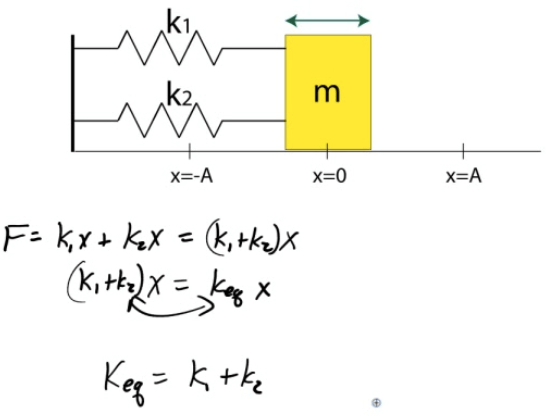
Springs in Parallel
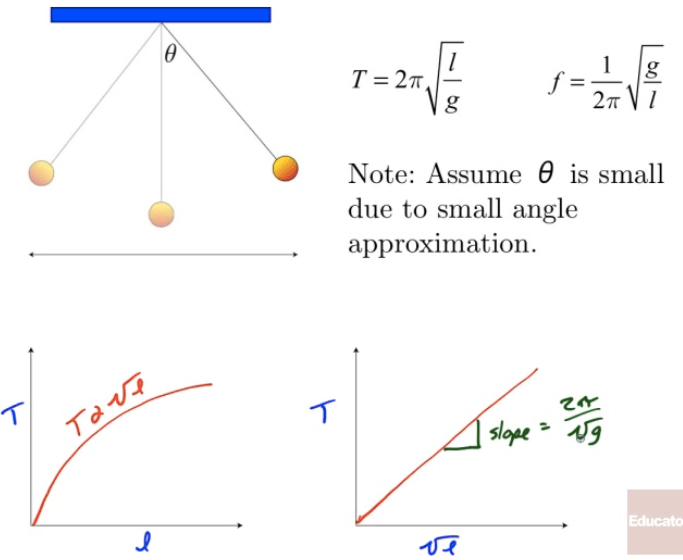
The Pendulum
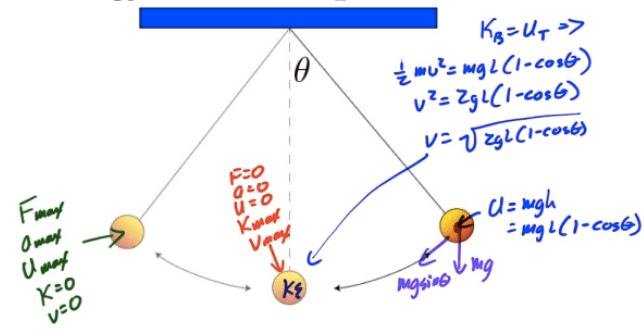
A mass m is attached to a light string that swings without friction about the vertical equilibrium position
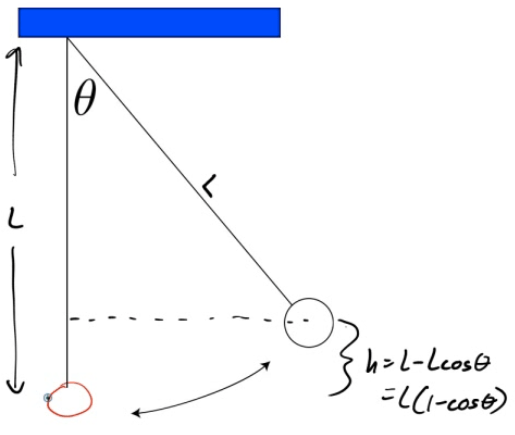
Energy and the Simple Pendulum
Frequency and Period of a Pendulum
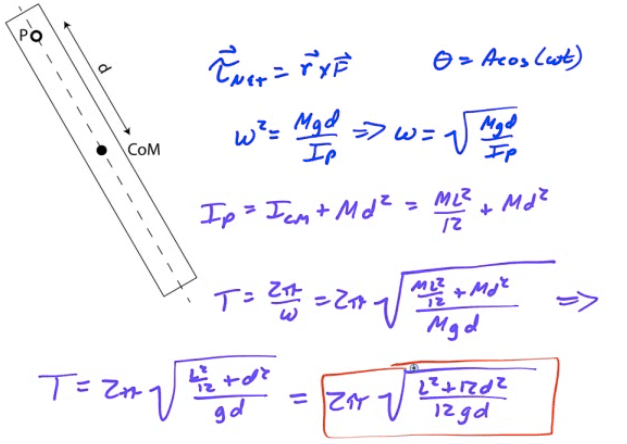
Period of a Physical Pendulum

Example 3: Deriving Period of a Simple Pendulum

Example 4: Deriving Period of a Physical Pendulum
Example 5: Summary of Spring-Block System
Example 6: Harmonic Oscillator Analysis
A 2-kg block is attacked to a spring. A force of 20 N stretches the spring to a displacement of 0.5 meter
The spring constant
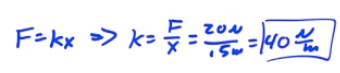
The total energy
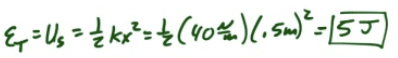
The speed at the equilibrium position
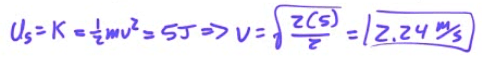
The speed at x=0.30 meters

The speed at x=-0.4 meters
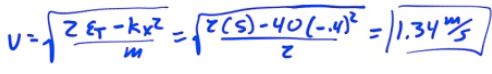
The acceleration at the equilibrium position

The magnitude of the acceleration at x=0.5 meters.
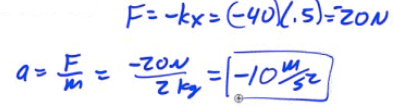
The net force at equilibrium position

The net force at x=0.25 meter
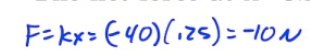
Where does kinetic energy = potential energy
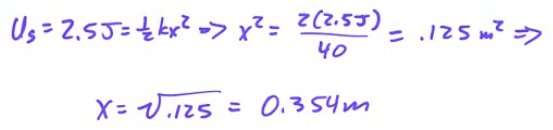
Example 7: Vertical Spring Block Oscillator
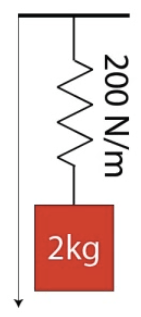
A 2-kg block attached to an un-stretched spring of spring constant k=200 N/m as shown in the diagram below is released from rest. Determine the period of the block's oscillation and the maximum displacement of the block from its equilibrium while undergoing simple harmonic motion.
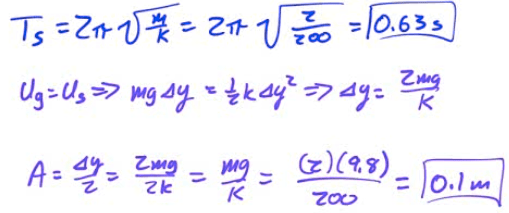
2009 Free Response Question 2

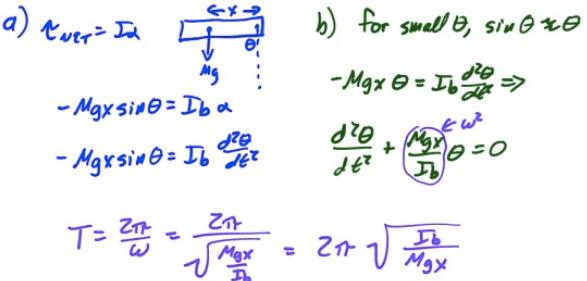
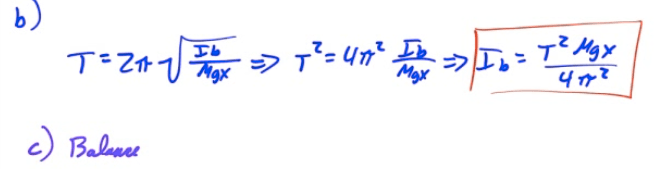
2010 Free Response Question 3